Consider a line and a circle that is tangent to the line. A second circle can be constructed that is also tangent to the line and that is tangent to the original circle. This construction will be demonstrated using a Geometer's Sketchpad construction.

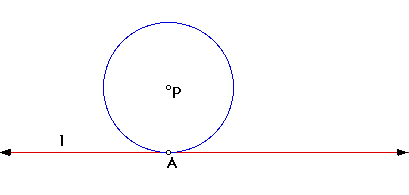
First, start with a line l and construct a point P that is not on the line. Construct another line m that is perpendicular to line l. Next, consturct a circle with center P that passes through the point of intersection (point A) of lines l and m. By doing this, you know that circle P is tangent to line l.

Now construct a point B that is on circle P, and construct line PB. At point B, construct a line n that is perpendicular to line PB. Locate point C which is the intersection point of lines n and l, and construct line segment AC. Now, construct point D so that C is the midpoint of line segment AD. Construct line r through point D that is perpendicular to line l and locate the point of intersection of lines r and line PB. This is point E, the center of the circle that is tangent to circle P and line l.

Finally, construct circle E tangent to circle P.

There are many circles that can be constructed in this way that are tangent to a given circle and a given line.

The locus of all of the center of such circles form a parabola. Click here to see a GSP demonstration. The vertex of the parabola is the point at which the original circle is tangent to the original line. The focal point of the parabola is the center of the original circle and the directorix is a line that is parallel to the original line and its distance from the original line is equal to the radius of the original circle. The directorix is on the side of the original line that is opposite from the original circle.

To see that this is true, refer to the diagram below.

Begin with a line l and a point P that is not on line l. Construct a line through point P that is perpendicular to line l at point A. Next construct a circle with center P and that passes through point A. Construct a point B that is on circle P and construct line PB. Construct a line through point B that is perpendicular to line PB so that it is tangent to circle P. Call the point at which this line intersects line l point C. Next, construct point D on line l so that C is the midpoint of AD. Construct a line through point D that is perpendicular to line l. The point at which this line intersects line PB is point E, the center of the desired circle.

Now quadrilateral PACB is a rhombus. and quadrilateral CDEB is also a rhombus and the two rhombi are similar.